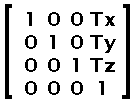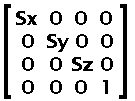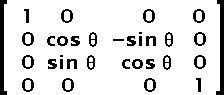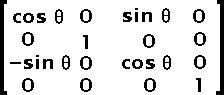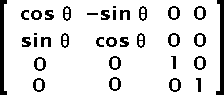Appendix A — The geometry in SWF — Matrix

The coordinates are often transformed with the use of a matrix. The matrix is similar to a transformation matrix in Postscript. It includes a set of scaling factors, rotation angles and translations.

When only the scaling factors are used (no rotation) then these are ratios as one would expect. If a rotation is also applied, then the scaling ratios will be affected accordingly.

The translations are in TWIPS like any coordinates and also they are applied last (thus, it represents the position at which the shape is drawn on the output screen).

The math formula is as simple as: Q = MP + T. Q is the resulting point, P is the source point, M is the scaling and rotation factors and T is the final translation.

With the use of a three dimensional set of matrices, one can compute a single matrix which includes all the transformations.

T = Fig 1. Matrix The Tx and Ty are set as defined in the SWF file. Tz can be set to zero. S = Fig 2. Matrix The Sx and Sy are set as defined in the SWF file when no rotation are defined. Sz is always set to 1. Rx = Fig 3. Matrix This matrix shows you a rotation over the X axis. This is not necessary for the SWF format. Ry = Fig 4. Matrix This matrix shows you a rotation over the Y axis. This is not necessary for the SWF format. Rz = Fig 5. Matrix This matrix shows you a rotation over the Z axis. This is used by the SWF format. However, it is mixed with the scaling factors. It is rare not to have a scaling factor when a rotation is applied.

Thus, the matrix saved in the SWF file is the product of the matrix in figure 2 and the matrix in figure 5.

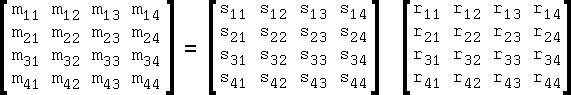
Fig 6. Matrix

A matrix multiplication is the sum of the products of rows (left matrix) and columns (right matrix).

	m11 = s11 * r11 + s12 * r21 + s13 * r31 + s14 * r41

	m12 = s21 * r11 + s22 * r21 + s23 * r31 + s24 * r41

	m13 = s31 * r11 + s32 * r21 + s33 * r31 + s34 * r41

	m14 = s41 * r11 + s42 * r21 + s43 * r31 + s44 * r41

	m21 = s11 * r12 + s12 * r22 + s13 * r32 + s14 * r42

	m22 = s21 * r12 + s22 * r22 + s23 * r32 + s24 * r42

	m23 = s31 * r12 + s32 * r22 + s33 * r32 + s34 * r42

	m24 = s41 * r12 + s42 * r22 + s43 * r32 + s44 * r42

	m31 = s11 * r13 + s12 * r23 + s13 * r33 + s14 * r43

	m32 = s21 * r13 + s22 * r23 + s23 * r33 + s24 * r43

	m33 = s31 * r13 + s32 * r23 + s33 * r33 + s34 * r43

	m34 = s41 * r13 + s42 * r23 + s43 * r33 + s44 * r43

	m41 = s11 * r14 + s12 * r24 + s13 * r34 + s14 * r44

	m42 = s21 * r14 + s22 * r24 + s23 * r34 + s24 * r44

	m43 = s31 * r14 + s32 * r24 + s33 * r34 + s34 * r44

	m44 = s41 * r14 + s42 * r24 + s43 * r34 + s44 * r44

Though you shouldn't need to find the scaling factors and rotation angle from an SWF matrix, it is possible to find one if you know the other. This is done using a multiplication of either the inverse scaling (use: 1/Sx and 1/Sy instead of Sx and Sy for the scaling matrix) or the inverse rotation (use: -angle instead of angle in the Z rotation matrix).

For those who still wonder what I'm talking about, there are the four computations you need from a scaling factor and an angle in radiant:

	SWFmatrix11 =  Sx * cos(angle)
	SWFmatrix12 =  Sy * sin(angle)
	SWFmatrix21 = -Sx * sin(angle)
	SWFmatrix22 =  Sy * cos(angle)

SWFmatrix11 and SWFmatrix22 are saved in the (x, y) scale respectively and the SWFmatrix21 and SWFmatrix12 are the rotation skew0 and skew1 values respectively.